Формула Шеннона
Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения "орла" и "решки" будут различаться.
Формулу для вычисления количества информации в случае различных вероятностей событий предложил К. Шеннон в 1948 году. В этом случае количество информации определяется по формуле:
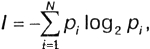 |
(2.2) |
где I - количество информации;
N - количество возможных событий;
рi - вероятность i-го события.
Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:
Р1 = 1/2, р2 = 1/4, р3 = 1/8, р4 = 1/8.
Тогда количество информации, которое мы получим после реализации одного из них, можно рассчитать по формуле (2.2):
I = -(l/2 log2l/2 + l/4 log2l/4 + l/8 log2l/8 + l/8 log2l/8) = (1/2 + 2/4 + 3/8 + 3/8) битов = 14/8 битов = 1,75 бита.
Этот подход к определению количества информации называется вероятностным.
Для частного, но широко распространенного и рассмотренного выше случая, когда события равновероятны (pi= 1/N), величину количества информации I можно рассчитать по формуле:
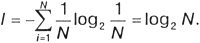 |
(2.3) |
По формуле (2.3) можно определить, например, количество информации, которое мы получим при бросании симметричной и однородной четырехгранной пирамидки:
I = log24 = 2 бита. Таким образом, при бросании симметричной пирамидки, когда события равновероятны, мы получим большее количество информации (2 бита), чем при бросании несимметричной (1,75 бита), когда события неравновероятны.
Количество информации, которое мы получаем, достигает максимального значения, если события равновероятны.
Выбор оптимальной стратегии в игре "Угадай число". На получении максимального количества информации строится выбор оптимальной стратегии в игре "Угадай число", в которой первый участник загадывает целое число (например, 3) из заданного интервала (например, от 1 до 16), а второй - должен "угадать" задуманное число. Если рассмотреть эту игру с информационной точки зрения, то начальная неопределенность знаний для второго участника составляет 16 возможных событий (вариантов загаданных чисел).
При оптимальной стратегии интервал чисел всегда должен делиться пополам, тогда количество возможных событий (чисел) в каждом из полученных интервалов будет одинаково и отгадывание интервалов равновероятно. В этом случае на каждом шаге ответ первого игрока ("Да" или "Нет") будет нести максимальное количество информации (1 бит).
Как видно из табл. 1.1, угадывание числа 3 произошло за четыре шага, на каждом из которых неопределенность знаний второго участника уменьшалась в два раза за счет получения сообщения от первого участника, содержащего 1 бит информации. Таким образом, количество информации, необходимое для отгадывания одного из 16 чисел, составило 4 бита.
| Таблица 2.1. Информационная модель игры "Угадай число" |
| Вопрос второго участника |
Ответ первого участника |
Неопределенность знаний (количество возможных событий) |
Полученное количество информации |
| |
|
16 |
|
| Число больше 8? |
Нет |
8 |
1 бит |
| Число больше 4? |
Нет |
4 |
1 бит |
| Число больше 2? |
Да |
2 |
1 бит |
| Число 3? |
Да |
1 |
1 бит |
|
Задания
1.3. Вычислить с помощью электронного калькулятора количество информации, которое будет получено:
- при бросании симметричного шестигранного кубика;
- при игре в рулетку с 72 секторами;
- при игре в шахматы игроком за черных после первого хода белых, если считать все ходы равновероятными;
- при игре в шашки.
1.4. Вероятность первого события составляет 0,5, а второго и третьего - 0,25. Какое количество информации мы получим после реализации одного из них?
1.5. Какое количество информации получит второй игрок в игре "Угадай число" при оптимальной стратегии, если первый игрок загадал число: от 1 до 64? От 1 до 128?
| 
