Материальные и информационные модели
Все модели можно разбить на два больших класса: материальные модели и информационные модели.
Материальные модели.
Предметные модели позволяют представить в материальной наглядной форме объекты и процессы, недоступные для непосредственного исследования (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы и др.).
Макеты зданий и сооружений позволяют архитекторам выбрать наилучшие градостроительные решения, модели самолетов и кораблей позволяют инженерам выбрать их оптимальную форму.
Предметные модели часто используются в процессе обучения. В курсе географии первые представления о нашей планете Земля мы получаем, изучая ее модель - глобус (рис. 4.3), в курсе физики изучаем работу двигателя внутреннего сгорания по его модели, в химии при изучении строения вещества используем модели молекул и кристаллических решеток, в биологии изучаем строение человека по анатомическим муляжам.
 |
| Рис. 4.3. Предметная модель - глобус Земли |
Информационные модели.
Информационные модели представляют объекты и процессы в образной или знаковой форме, а также в форме таблиц, блок-схем, графов и т. д.
Образные модели
Образные модели (рисунки, фотографии и др.) представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кинопленке и др.). Широко используются образные информационные модели в обучении, где требуется классификация объектов по их внешним признакам (вспомните учебные плакаты по ботанике, биологии и физике).
Графические информационные модели
Карта как информационная модель. Можно ли назвать информационной моделью карту местности (рис. 4.4)? Безусловно, можно! Во-первых, карта описывает конкретную местность, которая является для нее объектом моделирования. Во-вторых, это графическая информация. Карта создается с определенной целью: с ее помощью можно добраться до нужного населенного пункта. Кроме того, используя линейку и учитывая масштаб карты, можно определить расстояние между различными пунктами. Однако никаких более подробных сведений о населенных пунктах, кроме их положения, эта карта не дает.
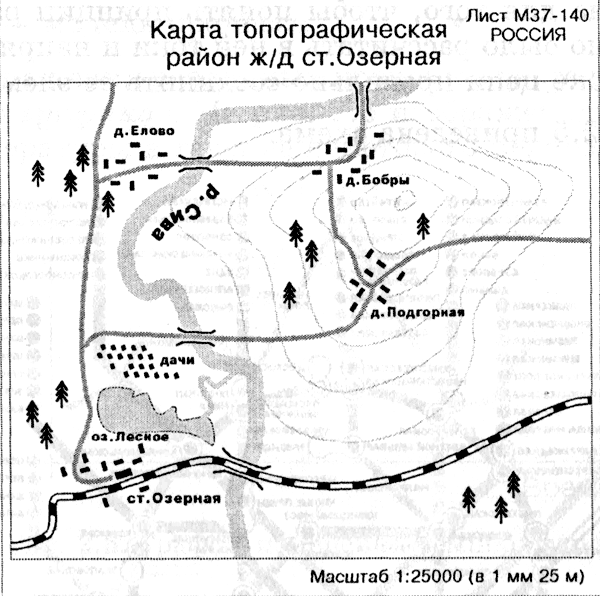 |
| Рис. 4.4. Карта местности |
Чертежи и схемы
Другими знакомыми вам примерами графических информационных моделей являются чертежи, схемы, графики.
Чертеж должен быть очень точным, на нем указываются все необходимые размеры. Например, чертеж болта нужен для того, чтобы, глядя на него, токарь мог выточить болт на станке (рис. 4.5).
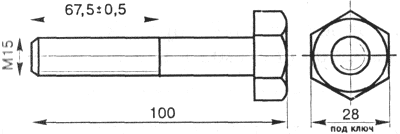 |
| Рис. 4.5. Чертеж болта |
У схемы электрической цепи нет никакого внешнего сходства с реальной электрической цепью (рис. 4.6). Электроприборы (лампочка, источник тока, конденсатор, сопротивление) изображены символическими значками, а линии - это соединяющие их проводники электрического тока. Электрическая схема нужна для того, чтобы понять принцип работы цепи, чтобы можно было рассчитать в ней токи и напряжения, чтобы при сборке цепи правильно соединить ее элементы.
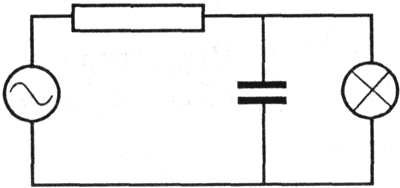 |
| Рис. 4.6. Схема электрической цепи |
На рис. 4.7 приведена схема.
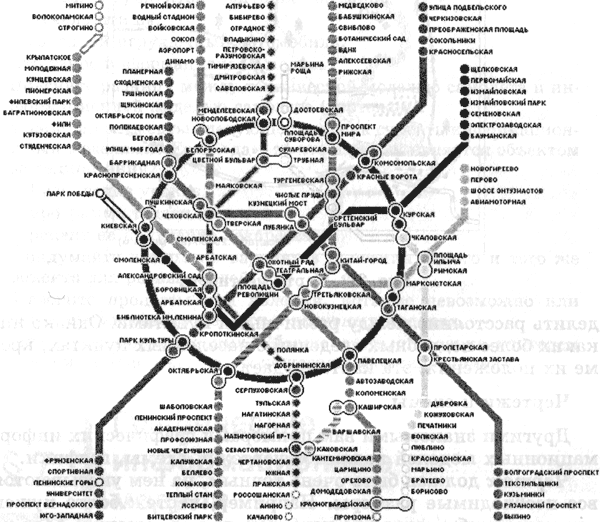 |
| Рис. 4.7. Схема московского метрополитена |
Схема - это графическое отображение состава и структуры сложной системы.
Структура - это определенный порядок объединения элементов системы в единое целое.
Структуру московского метрополитена называют радиально-кольцевой.
График - модель процесса.
Для отображения различных процессов часто прибегают к построению графиков. На рис. 4.8 изображен график изменения температуры в течение некоторого периода.
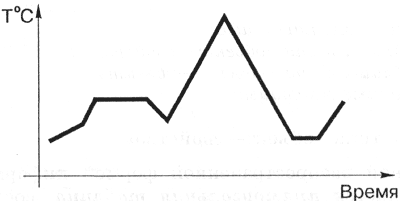 |
| Рис. 4.8. График изменения температуры |
С картами, чертежами, схемами, графиками вы имели дело и раньше. Просто раньше вы их не связывали с понятием информационной модели.
Знаковые информационные модели.
Знаковые информационные модели строятся с использованием различных языков (знаковых систем). Знаковая информационная модель может быть представлена в форме текста (например, программы на языке программирования) или формулы (например, второго закона Ньютона F = mа).
Табличные модели
Широко распространены информационные модели в форме таблиц. В таблице химических элементов Д. И. Менделеева химические элементы располагаются в ячейках таблицы по возрастанию атомных весов, а в столбцах - по количеству валентных электронов. Важно, что по положению в таблице можно определить некоторые физические и химические свойства элементов (рис. 4.9).
 |
| Рис. 4.9. Информационная модель - таблица элементов Д. И. Менделеева |
Таблицы типа "объект-свойство"
Еще одной распространенной формой информационной модели является прямоугольная таблица, состоящая из строк и столбцов. Использование таблиц настолько привычно, что для их понимания обычно не требуется дополнительных объяснений.
В качестве примера рассмотрим таблицу 4.1.
| Таблица 4.1. Домашняя библиотека |
| Номер |
Автор |
Название |
Год |
Полка |
| 0001 |
Беляев А.Р. |
Человек-амфибия |
1987 |
5 |
| 0002 |
Кервуд Д. |
Бродяги севера |
1991 |
7 |
| 0003 |
Тургенев И.С. |
Повести и рассказы |
1982 |
1 |
| 0004 |
Олеша Ю.К. |
Избранное |
1987 |
5 |
| 0005 |
Беляев А.Р. |
Звезда КЭЦ |
1990 |
5 |
| 0006 |
Тынянов Ю.Н. |
Кюхля |
1979 |
1 |
| 0007 |
Толстой Л.Н. |
Повести и рассказы |
1986 |
1 |
| 0008 |
Беляев А.Р. |
Избранное |
1994 |
7 |
|
При составлении таблицы в нее включается лишь та информация, которая интересует пользователя. Например, кроме тех сведений о книгах, которые включены в таблицу 4.1, существуют и другие: издательство, количество страниц, стоимость. Однако для составителя таблицы 4.1 было достаточно сведений, которые позволяют отличить одну книгу от другой (столбцы "Автор", "Название", "Год") и найти книгу на полках книжных стеллажей (столбец "Полка"). Предполагается, что все полки пронумерованы и, кроме того, каждой книге присвоен свой инвентарный номер (столбец "Номер").
Таблица 4.1 - это информационная модель книжного фонда домашней библиотеки.
Таблица может отражать некоторый процесс, происходящий во времени (табл. 4.2).
| Таблица 4.2. Погода |
| День |
Осадки |
Температура (градусы С) |
Давление (мм рт. ст.) |
Влажность (проценты) |
| 15.03.04 |
Снег |
-3,5 |
746 |
67 |
| 16.03.04 |
Без осадков |
0 |
750 |
62 |
| 17.03.04 |
Туман |
1,0 |
740 |
100 |
| 18.03.04 |
Дождь |
3,4 |
745 |
96 |
| 19.03.04 |
Без осадков |
5,2 |
760 |
87 |
|
Показания снимались в течение пяти дней в одно и то же время суток. Глядя на таблицу, легко сравнить разные дни по температуре, влажности и пр. Данную таблицу можно рассматривать как информационную модель процесса изменения состояния погоды.
Таблицы 4.1 и 4.2 относятся к наиболее часто используемому типу таблиц. Их будем называть таблицами типа "объект-свойство". В одной строке такой таблицы содержится информация об одном объекте (книга в библиотеке или состояние погоды в 12-00 в данный день). Столбцы - отдельные характеристики (свойства) объектов.
Конечно, строки и столбцы в таблицах 4.1 и 4.2 можно поменять местами, повернуть их на 90°. Иногда так и делают. Тогда строки будут соответствовать свойствам, а столбцы - объектам. Но чаще всего таблицы строят так, что строк в них больше, чем столбцов. Как правило, объектов больше, чем свойств.
Таблицы типа "объект-объект"
Другим распространенным типом таблиц являются таблицы, отражающие взаимосвязи между разными объектами. Назовем их таблицами типа "объект-объект". Вот понятный каждому школьнику пример таблицы успеваемости (табл. 4.3).
| Таблица 4.3. Успеваемость |
| Ученик |
Русский |
Алгебра |
Химия |
Физика |
История |
Музыка |
| Аликин Петр |
4 |
5 |
5 |
4 |
4 |
5 |
| Ботов Иван |
3 |
3 |
3 |
3 |
3 |
4 |
| Волков Илья |
5 |
5 |
5 |
5 |
5 |
5 |
| Галкина Нина |
4 |
4 |
5 |
2 |
4 |
4 |
|
Строки относятся к ученикам - это первый вид объектов; столбцы - к школьным предметам - второй вид объектов. В каждой клетке на пересечении строки и столбца - оценка, полученная данным учеником по данному предмету.
Таблица 4.4 тоже имеет тип "объект-объект". Однако, в отличие от предыдущей таблицы, в ней строки и столбцы относятся к одному и тому же виду объектов. В этой таблице содержится информация о наличии дорог между населенными пунктами .
| Таблица 4.4. Дороги |
| |
Дачи |
Озерная |
Подгорная |
Елово |
Бобры |
| Дачи |
1 |
1 |
1 |
1 |
0 |
| Озерная |
1 |
1 |
0 |
1 |
0 |
| Подгорная |
1 |
0 |
1 |
0 |
1 |
| Елово |
1 |
1 |
0 |
1 |
1 |
| Бобры |
0 |
0 |
1 |
1 |
1 |
|
Двоичные матрицы
В математике прямоугольная таблица, составленная из чисел, называется матрицей. Если матрица содержит только нули и единицы, то она называется двоичной матрицей. Числовая часть таблицы 4.4 представляет собой двоичную матрицу.
Таблица 4.5 также содержит двоичную матрицу.
| Таблица 4.5. Факультативы |
| Ученик |
Геология |
Цветоводство |
Танцы |
| Русанов |
1 |
0 |
1 |
| Семенов |
1 |
1 |
0 |
| Зотова |
0 |
1 |
1 |
| Шляпина |
0 |
0 |
1 |
|
В ней приведены сведения о посещении четырьмя учениками трех факультативов. Вам уже должно быть понятно, что единица обозначает посещение, ноль - непосещение. Из этой таблицы следует, например, что Русанов посещает геологию и танцы, Семенов - геологию и цветоводство и т. д.
В таблицах, представляющих собой двоичные матрицы, отражается качественный характер связи между объектами (есть дорога - нет дороги; посещает - не посещает и т. п.). Таблица 4.3 содержит количественные характеристики успеваемости учеников по предметам, выраженные оценками пятибалльной системы.
Мы рассмотрели только два типа таблиц: "объект-свойство" и "объект-объект". На практике используются и другие, гораздо более сложные таблицы.
При построении некоторых типов информационных моделей одновременно используются система графических элементов и знаковая система. Так, в блок-схемах алгоритмов используются различные геометрические фигуры для обозначения элементов алгоритма и формальный алгоритмический язык для записи инструкций программы (рис. 4.10).
Важную роль играют информационные модели, которые отображают иерархические системы. В биологии весь животный мир рассматривается как иерархическая система (тип, класс, отряд, семейство, род, вид), в информатике используется иерархическая файловая система и т. д.
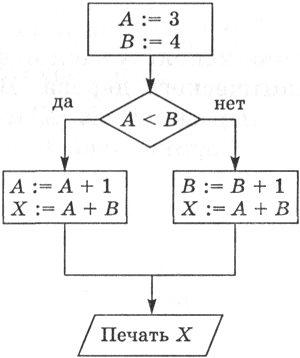 |
| Рис. 4.10. Информационная модель - блок-схема алгоритма |
В иерархической информационной модели объекты распределяются по уровням, от первого (верхнего) уровня до нижнего (последнего) уровня. На первом уровне может располагаться только один элемент. Основное отношение между уровнями состоит в том, что элемент более высокого уровня может состоять из нескольких элементов нижнего уровня, при этом каждый элемент нижнего уровня может входить в состав только одного элемента верхнего уровня.
Удобным способом наглядного представления иерархических информационных моделей являются графы. Элементы иерархической модели отображаются в графе овалами (вершинами графа).
Элементы каждого уровня, кроме последнего, находятся в отношении "состоять из" к элементам более низкого уровня. Такая связь между элементами отображается в форме дуги графа (направленной линии в форме стрелки).
Графы, имеющие одну вершину верхнего уровня, напоминают деревья, которые растут сверху вниз, поэтому называются деревьями. Дуги дерева могут связывать объекты только соседних иерархических уровней, причем каждый объект нижнего уровня может быть связан дугой только с одним объектом верхнего уровня.
Для описания исторического процесса смены поколений семьи используются информационные модели в форме генеалогического дерева. В качестве примера можно рассмотреть фрагмент (X-XI века) генеалогического дерева династии Рюриковичей (рис. 4.11).
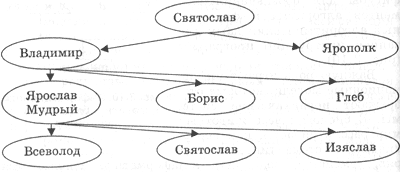 |
| Рис. 4.11. Информационная модель - генеалогическое дерево Рюриковичей (X-XI века) |
Контрольные вопросы
1. Какие вы можете назвать примеры материальных моделей?
2. Какие вы можете назвать примеры различных форм информационных моделей?
3. Приведите различные примеры графических информационных моделей.
4. Постройте графическую модель вашей квартиры. Что это: карта, схема, чертеж?
5. Какая форма графической модели (карта, схема, чертеж, график)
6. В чем состоит удобство табличного представления информации?
7. Приведите примеры таблиц, с которыми вам приходится иметь дело в школе и дома. Определите тип, к которому они относятся: "объект-свойство" или "объект-объект".
8. Что такое матрица? Что такое двоичная матрица?
Задания для самостоятельного выполнения
4.1. Задание с развернутым ответом. Построить фрагмент модели иерархической файловой системы вашего компьютера.
4.2. Задание с развернутым ответом. Построить фрагмент иерархической модели животного мира.
4.3. Задание с развернутым ответом. Построить фрагмент модели генеалогического дерева вашей семьи.
4.4. Постройте графическую модель собственной успеваемости по двум различным дисциплинам школьной программы (самой любимой и самой "нелюбимой"). Спрогнозируйте по этой модели свой дальнейший процесс обучения данным предметам.
4.5. Представьте в табличной форме сведения об увлечениях ваших одноклассников. Какой тип таблицы вы используете для этой цели?
4.6. Использование табличной модели часто облегчает решение информационной задачи. В следующей таблице закрашенные клетки в расписании занятий соответствуют урокам физкультуры в 9-11 классах школы.
| Расписание занятий |
| № урока |
9а |
9б |
10а |
10б |
11а |
11б |
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
Выполните следующие задания:
- определите, какое минимальное количество учителей физкультуры требуется при таком расписании;
- найдите один из вариантов расписания, при котором можно обойтись двумя учителями физкультуры;
- в школе три учителя физкультуры: Иванов, Петров, Сидоров; распределите между ними уроки в таблице так, чтобы ни у кого не было "окон" (пустых уроков);
- распределите между тремя учителями уроки так, чтобы нагрузка у всех была одинаковой.
6. В компьютерной сети узловым является сервер, с которым непосредственно связаны все остальные серверы. Дана следующая двоичная матрица. В ней С1, С2, СЗ, С4, С5 - обозначения серверов сети.
| |
С1 |
С2 |
С3 |
С4 |
С5 |
| С1 |
1 |
0 |
0 |
1 |
0 |
| С2 |
0 |
1 |
0 |
1 |
0 |
| С3 |
0 |
0 |
1 |
1 |
0 |
| С4 |
1 |
1 |
1 |
1 |
1 |
| С5 |
0 |
0 |
0 |
1 |
1 |
Определите, какой сервер является узловым.
| 
