2. Информационные системы в науке
2.1. Искусственные нейронные сети
Искусственные нейронные сети (ИНС) – вид математических моделей, которые строятся
по принципу организации и функционирования их биологических аналогов – сетей нервных
клеток (нейронов) мозга. В основе их построения лежит идея о том, что нейроны можно моделировать довольно простыми автоматами (называемыми искусственными нейронами), а вся
сложность мозга, гибкость его функционирования и другие важнейшие качества определяются
связями между нейронами (scintific.narod.ru, Диканев Т.В.).
История ИНС начинается с 1943 г., когда У. Маккалок и У. Питтс предложили первую
модель нейрона и сформулировали основные положения теории функционирования человеческого мозга. С тех пор теория прошла довольно большой путь, а что касается практики, то
годовой объем продаж на рынке ИНС в 1997 г. составлял 2 млрд. долл. с ежегодным приростом в 50 %.
Спрашивается, зачем нужны нейронные сети. Дело в том, что существует множество задач, которые трехлетний ребенок решает лучше, чем самые мощные вычислительные машины.
Рассмотрим, например задачу распознавания образов. Пусть у нас есть некоторая картинка
(дерево и кошка). Требуется понять, что на ней изображено и где. Если вы попробуете написать программу, решающую данную задачу, вам придется, последовательно перебирая отдельные пиксели этой картинки, в соответствии с некоторым критерием решить, какие из них принадлежат дереву, какие кошке, а какие ни тому, ни другому. Сформулировать же такой критерий, что такое дерево, – очень нетривиальная задача.
 |
| Рис. 9. Задача выделения и распознавания объектов на картинке (дерево, кошка) – пример трудно алгоритмизируемой задачи |
Тем ни менее мы легко распознаем деревья, и в жизни и на картинках, независимо от точки зрения и освещенности. При этом мы не формулируем никаких сложных критериев. В свое время родители показали нам,
что это такое, и мы поняли. На этом примере можно сформулировать несколько принципиальных отличий в
обработке информации в мозге и в обычной вычислительной машине:
1) способность к обучению на примерах;
2) способность к обобщению, т.е. мы, не просто запомнили все примеры виденных деревьев, мы создали в мозгу некоторый идеальный образ абстрактного дерева. Сравнивая с
ним любой объект, мы сможем сказать, похож он на дерево или нет;
3) еще одно видное на этой задаче отличие – это параллельность обработки информации. Мы не считываем картинку по пикселям, мы видим ее целиком и наш мозг целиком ее и
обрабатывает;
4) поразительная надежность нашего мозга. К старости некоторые структуры мозга теряют до 40 % нервных клеток. При этом многие остаются в здравом уме и твердой памяти;
5) ассоциативность нашей памяти – это способность находить нужную информацию по
ее малой части.
Хотелось бы понять, какие именно особенности организации позволяют мозгу работать
столь эффективно. Рассмотрим вкратце, как он устроен. Все, наверное, знают, что мозг состоит из нервных клеток (нейронов). Всего их ~1012 штук. Основные из этих особенностей –
это:
6) адаптивность;
7) толерантность (терпимость) к ошибкам;
8) низкое энергопотребление.
Можно предположить, что приборы, построенные на тех же принципах, что и биологические нейроны, будут обладать перечисленными характеристиками.
Изобразим схематично отдельный нейрон. Он имеет один длинный, ветвящийся на конце отросток – аксон и множество мелких ветвящихся отростков – дендритов (рис. 10). Из-
вестно, что в ответ на возбуждение нейрон может генерировать нервный импульс, распространяющийся вдоль аксона. О его природе вам должны были рассказывать в курсе биофизики, т.е. это волна деполяризации мембраны нейрона. Она является автоволной, т.е. ее форма и скорость распространения не зависят от того, как и из-за чего она возникла. Доходя до
конца аксона, она вызывает выделение веществ, называемых нейромедиаторами. Воздействуя на дендриты других нейронов, они могут в свою очередь вызвать появление в них нервных импульсов.
4. Машина фон Неймана по сравнению с биологической
нейронной системой (www.osp.ru)
| Показатели |
Машина фон Неймана |
Биологическая нейронная система |
| Процессор |
Сложный |
Простой |
| Высокоскоростной |
Низкоскоростной |
| Один или несколько |
Большое количество |
| Память |
Отделена от процессора |
Интегрирована в процессор |
| Локализована |
Распределенная |
| Адресация не по содержанию |
Адресация по содержанию |
Вычисления |
Централизованные |
Распределенные |
| Последовательные |
Параллельные |
| Хранимые программы |
Самообучение |
Надежность |
Высокая уязвимость |
Живучесть |
Специализация |
Численные и символьные операции |
Проблемы восприятия |
Среда функционирования |
Строго определенная |
Плохо определенная |
| Строго ограниченная |
Без ограничений |
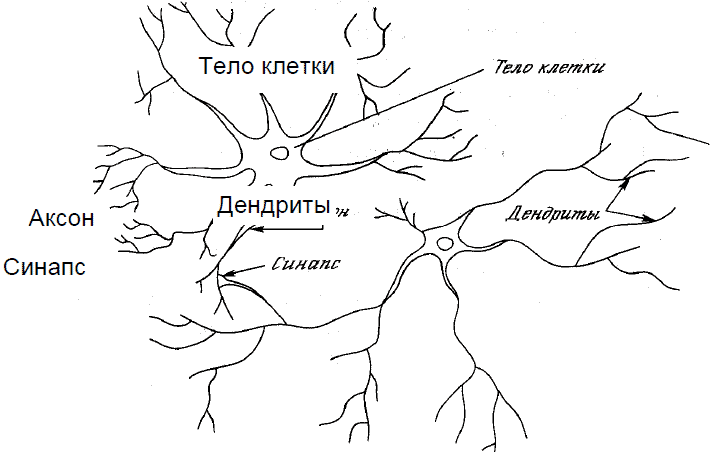 |
| Рис. 10. Биологический нейрон |
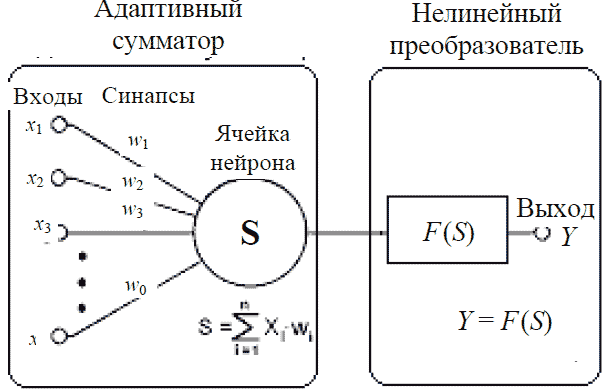 |
| Рис. 11. Искусственный нейрон |
Давайте запишем, что нейрон является типичным элементом, действующим по принципу
"все или ничего". Когда суммарный сигнал, приходящий от других нейронов, превышает некоторое пороговое значение, генерируется стандартный импульс. В противном случае нейрон остается в состоянии покоя.
Биологический нейрон – сложная система, математическая модель которой до конца не
построена. В основе теории ИНС лежит предположение о том, что вся эта сложность несущественна, а свойства мозга объясняются характером их соединения. Поэтому вместо точных математических моделей нейронов используется простая модель так называемого формального нейрона.
Он имеет входы, куда подаются некоторые числа x1, …, xn . Затем стоит блок, называе-
мый адаптивным сумматором. На его выходе мы имеем взвешенную сумму входов:
|
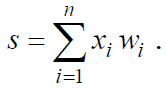
| (l) |
Затем она подается на нелинейный преобразователь и на выходе мы имеем:
Функция F нелинейного преобразователя называется активационной функцией нейрона.
Исторически первой была модель, в которой в качестве активационной функции использова-
лась ступенчатая функция или функция единичного скачка:
|
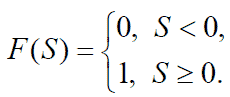
| (3) |
То есть по аналогии с биологическим нейроном, когда суммарное воздействие на входе превысит критическое значение, генерируется импульс 1. Иначе нейрон остается в состоянии покоя, т.е. выдается 0.
Существует множество других функций активации. Одной из наиболее распространенных является логистическая функция (сигмоид).
|
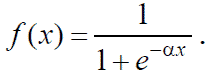
| (4) |
При уменьшении α сигмоид становится более пологим, в пределе привырождаясь
в горизонтальную линию на уровне 0,5, при увеличении сигмоид приближается по внешнему виду к функции единичного скачка с порогом в точке x = 0. Одно из ценных свойств
сигмоидной функции – простое выражение для ее производной.
|
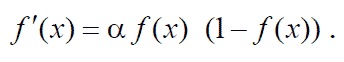
| (5) |
Теперь рассмотрим, как из таких нейронов можно составлять сети из таких нейронов.
Строго говоря, как угодно, но такой произвол слишком необозрим. Поэтому выделяют несколько стандартных архитектур, из которых путем вырезания лишнего или добавления
строят большинство используемых сетей. Можно выделить две базовые архитектуры: полносвязные и многослойные сети.
В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в
том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут
быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.
В многослойных нейронных сетях (их часто называют персептронами) нейроны объединяются в слои.
Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть
любым и не зависит от количества нейронов в других слоях. В общем случае сеть состоит из нескольких слоев,
пронумерованных слева на право. Внешние входные сигналы подаются на входы нейронов входного слоя (его
часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и
выходного слоев в многослойной нейронной сети есть один или несколько так называемых скрытых слоев.
В свою очередь, среди многослойных сетей выделяют:
1) Сети прямого распространения (feedforward networks) – сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и
так далее вплоть до выходного, который выдает сигналы для интерпретатора и пользователя. Если не оговорено
противное, то каждый выходной сигнал n-го слоя передастся на вход всех нейронов (n + 1)-го слоя; однако возможен вариант соединения n-го слоя с произвольным (n + p)-м слоем. Пример слоистой сети представлен на
рис. 4.
2. Сети с обратными связями (recurrent networks). В сетях с обратными связями информация передается с последующих слоев на предыдущие. Следует иметь в виду, что после
введения обратных связей сеть уже не просто осуществляет отображение множества входных векторов на множество выходных, она превращается в динамическую систему и возникает вопрос об ее устойчивости.
Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически
оно ограничено ресурсами компьютера или специализированных микросхем, на которых обычно реализуется
нейросеть. Чем сложнее сеть, тем более сложные задачи она может решать.
Искусственные нейронные сети могут широко использоваться в различных областях, вопрос в том, как подобрать такие весовые коэффициенты, чтобы сеть, например, решала задачу распознавания или аппроксимировала некоторую функцию. Замечательное свойство нейронных сетей состоит в том, что их этому можно научить.
Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке.
Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети
обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.
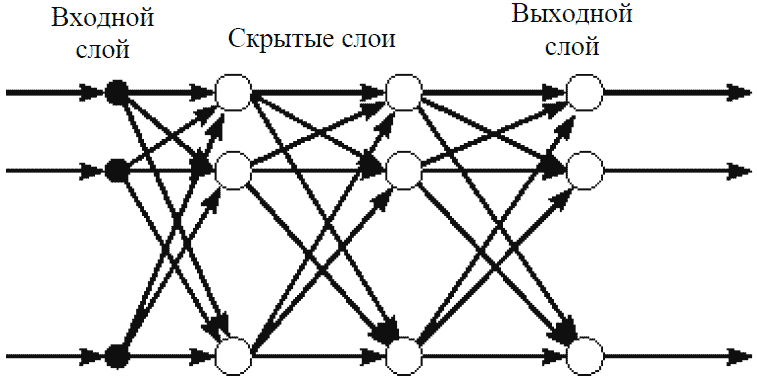 |
| Рис. 12. Многослойная (трехслойная) сеть прямого распространения |
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть – знать доступную для сети информацию. Эта модель определяет парадигму обучения [3]. Во-вторых, необходимо понять, как модифицировать весовые параметры сети – какие правила
обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются
правила обучения для настройки весов.
Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом
случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса
настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам.
Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности
выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура
данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением
по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия
решений могут быть на ней сформированы. Сложность образцов определяет число обучащих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо – на тестовых примерах, подчиненных тому
же статистическому распределению.
Контрольные вопросы к разделу 2.1
1. Что такое "искусственные нейронные сети" (ИНС)?
2. Приведите пример использования ИНС для распознавания образов?
3. Сформулируйте несколько принципиальных отличий в обработке информации в мозге
человека и в обычной вычислительной машине.
4. Сравните машину фон Неймана и биологическую нейронную систему.
5. Расскажите о биологическом нейроне и о его математической модели – искусственном нейроне.
6. Расскажите о полносвязных и многослойных нейронных сетях.
7. Какие сети выделяют среди многослойных нейронных сетей?
8. Расскажите, для чего применяется процесс обучения нейронных сетей.
9. Какие существуют парадигмы обучения ИНС?
| 
